How to Use the CRA model to Teach Math Fact Fluency
We know that math fact fluency is essential for our students' success in math. We also know that mental math strategies are highly effective in accelerating math fact fluency.
So, we know why we are teaching to mastery,
we know what to teach for mastery,
are you wondering how to teach these effective strategies?
I know I was sure was wondering as I watched so many of my students struggled to master the basic addition and subtraction facts.
The answer to ‘How': Use CRA sequence of instruction.

What is the CRA Sequence of Instruction?
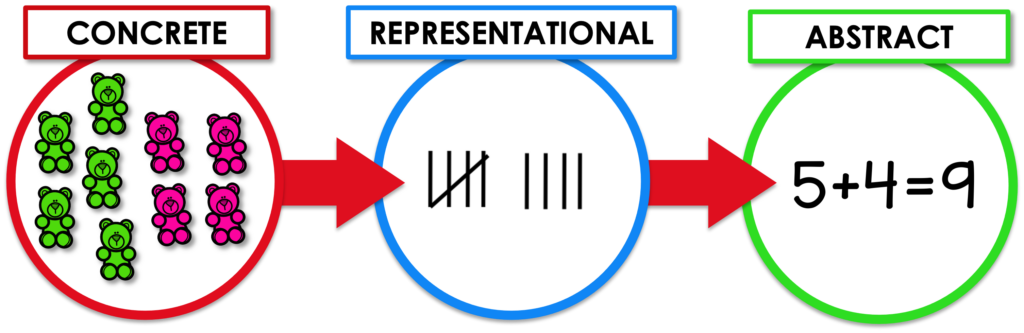
The CRA Sequence of Instruction is an instructional model that leads the students through 3 different phases of relating to math concepts: Concrete, Representational, Abstract.
Research confirms that students develop a deeper understanding of a concept when they move through the levels of understanding in the structured Concrete, Representational, Abstract (CRA) model.
CRA has its roots in the work of Bruner (1966). Marietta Barton introduced the model to me in her Math Their Way (1975) book and training. It transformed my understanding of how people learn! I immediately applied it to my teaching of math fact fluency.
All students benefit from learning with this model; however, students who struggle in math benefit and flourish! This model effectively teaches all math concepts, but I will be using it to teach mental math strategies in this article.
So, let's take a closer look at what it is and how to use the CRA model to teach math fact fluency.
I like to use math mats to move students through the 3 phases of the CRA model.
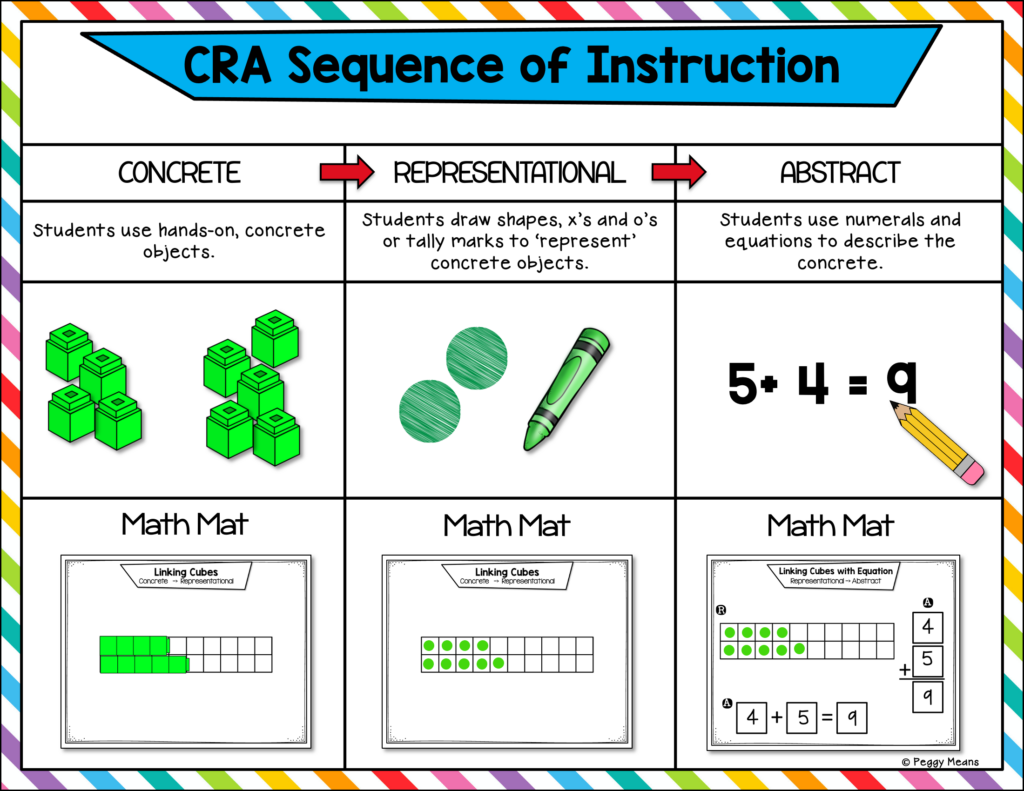
This table illustrates how to teach the ‘Doubles Plus One' strategy through the phases of the CRA model.
CONCRETE Phase of CRA Model of Instruction

Hands-On, Doing
This is the phase where students use concrete objects to interact with the concept being presented.
Acting out math situations is also a fun and effective activity at this phase.
This is an important phase because it provides the opportunity for students to make tactile and kinesthetic neuropathways creating the foundation for concept formation.
Give the student many opportunities to practice the concept using a variety of manipulatives. We want to be sure that students understand the concept at this Concrete phase before moving to the Representational phase.
Some student favorites:
- Colored chips
- Beans
- Linking cubes
- Popsicle sticks
- Buttons
- Rocks
- Bears
- Mini erasers
- Pom poms
REPRESENTATIONAL (Pictorial) Phase of CRA Model of Instruction
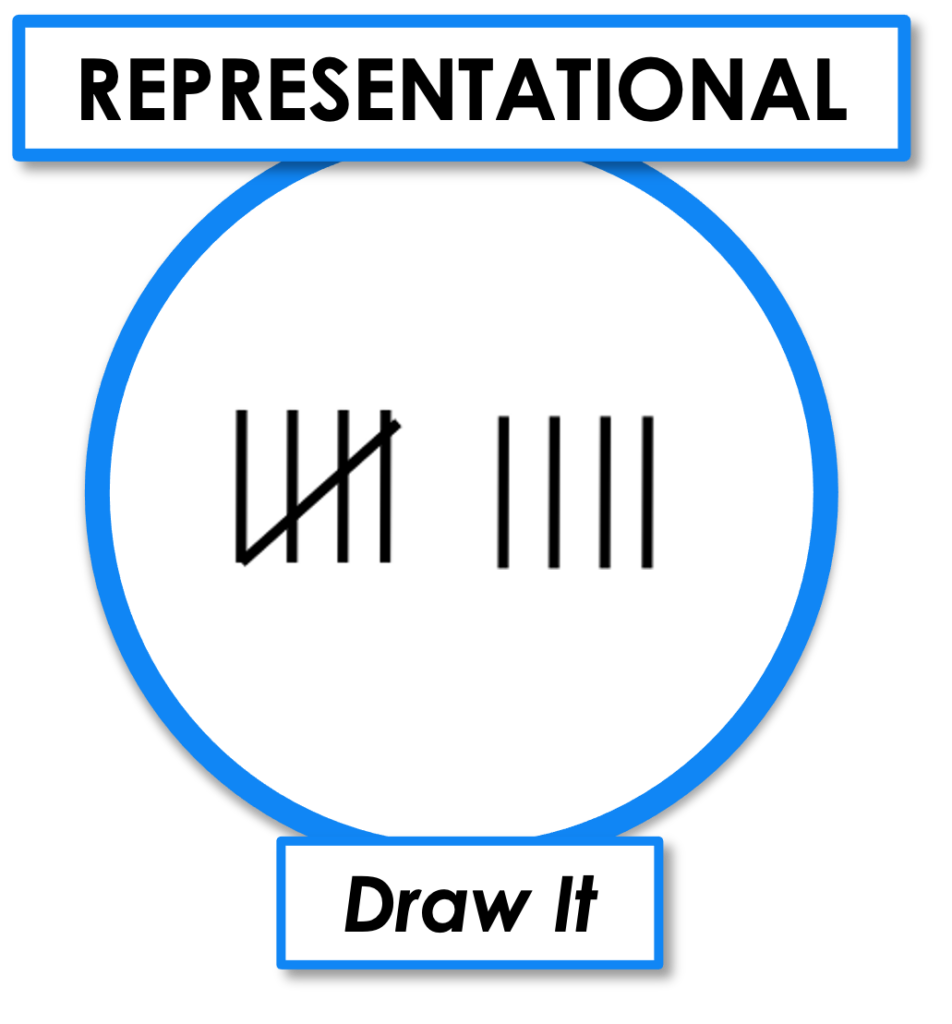
Draw It
The student will refer to their concrete model as they use drawings in the place of the concrete objects.
This is the all-important transitional phase. Don’t be in a rush to skip this phase. This is when the brain makes connections and embeds the new learning deeper into long-term memory. Introduce the use of pictures, tally marks, dots, circles, or diagrams to represent the concrete manipulatives.
ABSTRACT Phase of CRA Model of Instruction

Write It
As your students become comfortable and familiar with the math concept through the Concept and Representational phases, it is time to introduce the Abstract learning phase. Students will now use digits and symbols to represent their thinking.
This is the place I used to start with before I was introduced to the CRA teaching model. (true confession). In actuality, it needs to be the last phase because the first two laid the foundation (neuropathways) for success at this level.
The CRA model provides a framework that leads students through 3 phases of learning: Concrete, Representational, and Abstract. It is a highly effective teaching model, and it is fun for your students by providing engaging activities allowing them to feel successful – and to master those math facts!
I have created lessons that teach addition and subtraction mental math strategies that utilize the CRA model. I invite you to check them out .
RELATED RESOURCES
PIN FOR LATER








 My name is Peggy Means. I am a child of God and a retired elementary teacher. I loved teaching and creating engaging resources for my students. Now, I love sharing my resources and ideas with busy teachers around the world.
My name is Peggy Means. I am a child of God and a retired elementary teacher. I loved teaching and creating engaging resources for my students. Now, I love sharing my resources and ideas with busy teachers around the world.




